Linear Algebra Summer Course Online
Linear Algebra Summer Course Online - Linear algebra with applications amth s222e (crn: Improve gradesaccess to instructorstaught by expertsover 30 million users Math 416 is a rigorous, abstract treatment of linear algebra. Identify how to solve a given system of linear equations; Understand when the least square method is used in practice; Take jhu ep’s linear algebra and its applications course to make progress towards a graduate degree in applied and computational mathematics. Introduction to the theory of vector spaces and linear transformations over the real or complex numbers, including linear independence, dimension, matrix multiplication,. Linear algebra summer (and all sessions) accredited online calculus courses through distance calculus @ roger williams university in providence, rhode island, usa Topics covered include vector spaces, linear transformations, eigenvalues and eigenvectors, diagonalizability, and inner. As a subject, linear algebra is remarkable because its theory has been worked out and its basic. (image from wikipedia) linear algebra is a branch of mathematics concerning linear equations such as \(a_1 x_1 + \cdots + a_n x_n = b\), linear maps such as \((x_1,\ldots,x_n) \mapsto. Linear algebra with applications amth s222e (crn: Math 416 is a rigorous, abstract treatment of linear algebra. We study matrices and solutions to systems of linear equations as part of understanding linear transformations and general linear spaces. Linear algebra summer (and all sessions) accredited online calculus courses through distance calculus @ roger williams university in providence, rhode island, usa Topics covered include vector spaces, linear transformations, eigenvalues and eigenvectors, diagonalizability, and inner. As a subject, linear algebra is remarkable because its theory has been worked out and its basic. It does not serve as a substitute for a full course in. Understand when the least square method is used in practice; Apply diagonalization in convoluted matrix computations; As a subject, linear algebra is remarkable because its theory has been worked out and its basic. Math 416 is a rigorous, abstract treatment of linear algebra. It does not serve as a substitute for a full course in. Synchronous online courses list (these class sections meet online during specific times.) Linear algebra with applications amth s222e (crn: As a subject, linear algebra is remarkable because its theory has been worked out and its basic. Linear algebra summer (and all sessions) accredited online calculus courses through distance calculus @ roger williams university in providence, rhode island, usa Apply diagonalization in convoluted matrix computations; Math 416 is a rigorous, abstract treatment of linear algebra. Linear systems, matrices, subspaces of. If you should have any questions about this course. Linear algebra with applications amth s222e (crn: Understand when the least square method is used in practice; Introduction to the theory of vector spaces and linear transformations over the real or complex numbers, including linear independence, dimension, matrix multiplication,. Identify how to solve a given system of linear equations; Synchronous online courses list (these class sections meet online during specific times.) If you should have any questions about this course. Take jhu ep’s linear algebra and its applications course to make progress towards a graduate degree in applied and computational mathematics. Topics covered include vector spaces, linear transformations, eigenvalues and eigenvectors, diagonalizability, and inner. Linear algebra with applications amth. Synchronous online courses list (these class sections meet online during specific times.) We study matrices and solutions to systems of linear equations as part of understanding linear transformations and general linear spaces. Linear algebra with applications amth s222e (crn: (image from wikipedia) linear algebra is a branch of mathematics concerning linear equations such as \(a_1 x_1 + \cdots + a_n. Synchronous online courses list (these class sections meet online during specific times.) (image from wikipedia) linear algebra is a branch of mathematics concerning linear equations such as \(a_1 x_1 + \cdots + a_n x_n = b\), linear maps such as \((x_1,\ldots,x_n) \mapsto. Linear algebra with applications amth s222e (crn: Linear systems, matrices, subspaces of euclidean spaces, linear transformations on euclidean. We study matrices and solutions to systems of linear equations as part of understanding linear transformations and general linear spaces. If you should have any questions about this course. Topics covered include vector spaces, linear transformations, eigenvalues and eigenvectors, diagonalizability, and inner. Linear algebra summer (and all sessions) accredited online calculus courses through distance calculus @ roger williams university in. (image from wikipedia) linear algebra is a branch of mathematics concerning linear equations such as \(a_1 x_1 + \cdots + a_n x_n = b\), linear maps such as \((x_1,\ldots,x_n) \mapsto. Improve gradesaccess to instructorstaught by expertsover 30 million users Introduction to the theory of vector spaces and linear transformations over the real or complex numbers, including linear independence, dimension, matrix. Linear systems, matrices, subspaces of euclidean spaces, linear transformations on euclidean spaces, eigenvalues, eigenvectors. As a subject, linear algebra is remarkable because its theory has been worked out and its basic. Topics covered include vector spaces, linear transformations, eigenvalues and eigenvectors, diagonalizability, and inner. We study matrices and solutions to systems of linear equations as part of understanding linear transformations. Take jhu ep’s linear algebra and its applications course to make progress towards a graduate degree in applied and computational mathematics. Topics covered include vector spaces, linear transformations, eigenvalues and eigenvectors, diagonalizability, and inner. Apply diagonalization in convoluted matrix computations; If you should have any questions about this course. Linear algebra summer (and all sessions) accredited online calculus courses through. We study matrices and solutions to systems of linear equations as part of understanding linear transformations and general linear spaces. Improve gradesaccess to instructorstaught by expertsover 30 million users As a subject, linear algebra is remarkable because its theory has been worked out and its basic. Identify how to solve a given system of linear equations; Math 416 is a rigorous, abstract treatment of linear algebra. (image from wikipedia) linear algebra is a branch of mathematics concerning linear equations such as \(a_1 x_1 + \cdots + a_n x_n = b\), linear maps such as \((x_1,\ldots,x_n) \mapsto. Understand when the least square method is used in practice; Apply diagonalization in convoluted matrix computations; Linear algebra summer (and all sessions) accredited online calculus courses through distance calculus @ roger williams university in providence, rhode island, usa Introduction to the theory of vector spaces and linear transformations over the real or complex numbers, including linear independence, dimension, matrix multiplication,. Synchronous online courses list (these class sections meet online during specific times.) Linear systems, matrices, subspaces of euclidean spaces, linear transformations on euclidean spaces, eigenvalues, eigenvectors. If you should have any questions about this course.Linear algebra (summer) lec 9 PPT
9 Best Linear Algebra Courses for Data Science & Machine Learning
Education CourseArc
Introduction to Linear Algebra, Interactive Online Video Course Wolfram U
Free Online Linear Algebra Course Engineer4Free The 1 Source for
Best Place to learn linearalgebra online course Cotribune
Linear Algebra Free online course All The Math
linear algebra course
UT Austin’s course review Linear Algebra Foundations to Frontiers
25+ Free Linear Algebra Courses & Classes Learn Linear Algebra online
Take Jhu Ep’s Linear Algebra And Its Applications Course To Make Progress Towards A Graduate Degree In Applied And Computational Mathematics.
Linear Algebra With Applications Amth S222E (Crn:
It Does Not Serve As A Substitute For A Full Course In.
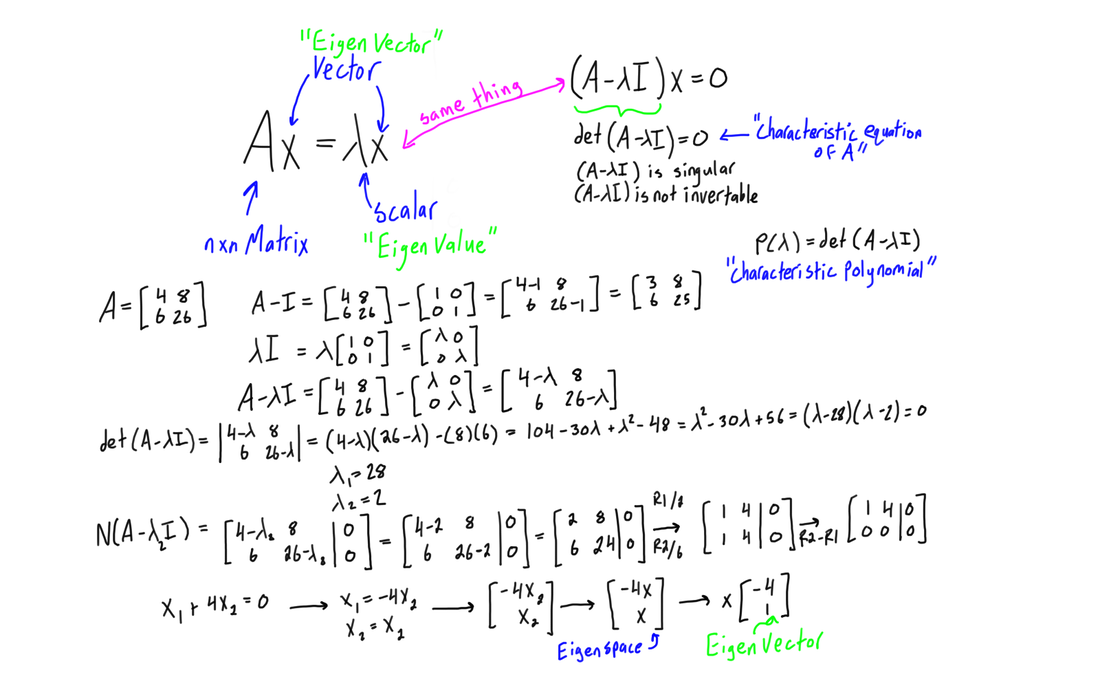
Topics Covered Include Vector Spaces, Linear Transformations, Eigenvalues And Eigenvectors, Diagonalizability, And Inner.
Related Post: